报告题目：2D Coulomb Gases and Their Statistical Behaviors

报告人：杨孟（大湾区大学）

报告时间：2025年4月25日星期五上午10:00-11:30

报告地点：数学与统计学院235教室

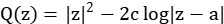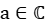报告摘要:We consider 2D Coulomb gases with the external potential , where and . Equivalently, this model can be realised as N eigenvalues of the complex Ginibre matrix of size  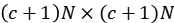conditioned to have deterministic eigenvalue a with multiplicity 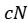. Depending on the values of  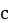and 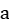, the droplet reveals a phase transition: it is doubly connected in the post-critical regime and simply connected in the pre-critical regime. In both regimes, we derive precise large-N expansions of the free energy up to the O(1) term, providing a non-radially symmetric example that confirms the Zabrodin-Wiegmann conjecture made for general planar Coulomb gas ensembles. As a consequence, our results provide asymptotic behaviours of moments of the characteristic polynomial of the complex Ginibre matrix, where the powers are of order O(N). Furthermore, by combining with a duality formula, we obtain precise large deviation probabilities of the smallest eigenvalue of the Laguerre unitary ensemble. This talk is based on the joint work with Sung-Soo Byun and Seong-Mi Seo.

报告人简介：杨孟，大湾区大学助理教授。博士毕业于美国南佛罗里达大学，曾在比利时法语鲁汶大学和丹麦哥本哈根大学从事博士后研究。主要研究领域为：数学物理、随机矩阵理论等。相关科研成果发表在Comm. Pure Appl. Math.、Comm. Math. Phys.、Int. Math. Res. Not.、SIAM J. Math. Anal.、J. Phys. A等国际