报告题目:Riemannian Smoothing Gradient Type Algorithms for Nonsmooth Optimization Problem on Compact Riemannian Submanifold Embedded in Euclidean Space
报 告人:彭 拯(湘潭大学)
报告时间:2024年12月23日15:30-16:30
地 点:数学与统计学院245会议室
报告摘要:In this paper, we introduce the notion of generalized  -stationarity for a class of nonconvex and nonsmooth composite minimization problems on compact Riemannian submanifold embedded in Euclidean space. To find a generalized
-stationarity for a class of nonconvex and nonsmooth composite minimization problems on compact Riemannian submanifold embedded in Euclidean space. To find a generalized  -stationarity point, we develop a family of Riemannian gradient-type methods based on the Moreau envelope technique with a decreasing sequence of smoothing parameters, namely Riemannian smoothing gradient and Riemannian smoothing stochastic gradient methods. We prove that the Riemannian smoothing gradient method has the iteration complexity of
-stationarity point, we develop a family of Riemannian gradient-type methods based on the Moreau envelope technique with a decreasing sequence of smoothing parameters, namely Riemannian smoothing gradient and Riemannian smoothing stochastic gradient methods. We prove that the Riemannian smoothing gradient method has the iteration complexity of 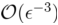 for driving a generalized
for driving a generalized  -stationary point. To our knowledge, this is the best-known iteration complexity result for the nonconvex and nonsmooth composite problem on manifolds. For the Riemannian smoothing stochastic gradient method, one can achieve the iteration complexity of
-stationary point. To our knowledge, this is the best-known iteration complexity result for the nonconvex and nonsmooth composite problem on manifolds. For the Riemannian smoothing stochastic gradient method, one can achieve the iteration complexity of 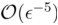 for driving a generalized
for driving a generalized  -stationary point.
-stationary point.
 彭拯,湘潭大学数学与计算科学学院教授,博士生导师。主要从事数学优化理论、算法及其应用研究,当前研究兴趣在于流形优化与流形学习,以及超大规模集成电路物理设计、下一代通信网络、新能源电力系统等理论与实际应用中的大规模非凸非光滑优化问题的求解算法,尤其关注大规模优化问题的随机优化算法与非单调优化算法相关研究。主持国家重要科研项目6项,省部级项目5项。当前兼任中国运筹学会常务理事、湖南省运筹学会副理事长,中国运筹学会算法软件及其应用分会常务理事和数学规划分会理事。
彭拯,湘潭大学数学与计算科学学院教授,博士生导师。主要从事数学优化理论、算法及其应用研究,当前研究兴趣在于流形优化与流形学习,以及超大规模集成电路物理设计、下一代通信网络、新能源电力系统等理论与实际应用中的大规模非凸非光滑优化问题的求解算法,尤其关注大规模优化问题的随机优化算法与非单调优化算法相关研究。主持国家重要科研项目6项,省部级项目5项。当前兼任中国运筹学会常务理事、湖南省运筹学会副理事长,中国运筹学会算法软件及其应用分会常务理事和数学规划分会理事。
